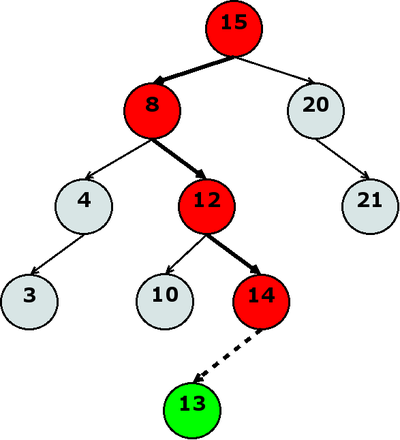
Рис. 1: добавление элемента
![[info]](http://p-stat.livejournal.com/img/openid-profile.gif){kind=small}
redchrom-ом, где он
усомнился в целесообразности использования функционального стиля, мол,
"мозг просаживает и производительность падает" :) Ниже я попробую
опровергнуть эти утверждения (насколько это у меня получится) -- я
попробую показать, что писать в функциональном стиле на схеме не
просто легко и приятно, но и штраф в производительности мы
получаем более, чем терпимый.
(fold + 0 '(1 2 3 4)) |
(define (fold proc acc list)
(if (null? list)
acc
(fold proc (proc (car list) acc) (cdr list))))
|
(define (1+ x) (+ x 1)) (unfold 0 (lambda (x) (>= x 10)) 1+) |
(define (unfold init end? next)
(let loop ((value init) (list '()))
(if (end? value)
(reverse list)
(loop (next value) (cons value list)))))
|
for (int i = 0; i < my_size; i++)
do_something( my_array[i] );
|
struct point3d_t
{
int x;
int y;
int z;
};
|
(define (make-point3d x y z) (list x y z)) (define (point3d-x point) (car point)) (define (point3d-y point) (cadr point)) (define (point3d-z point) (caddr point)) (define-macro (with-point3d point . body) `(apply (lambda (x y z) ,@body) ,point)) |
Хозяйке на заметкуЕсли ваш интерпретатор схемы не поддерживает макросы в стиле Common Lisp (define-macro), можно воспользоваться стандартным схемовским define-syntax, поменяв синтаксис макроса |
(define (make-point3d x y z)
(list->vector (list x y z)))
(define (point3d-x point) (vector-ref point 0))
(define (point3d-y point) (vector-ref point 1))
(define (point3d-z point) (vector-ref point 2))
(define-macro (with-point3d point . body)
`(let ((x (point3d-x ,point))
(y (point3d-y ,point))
(z (point3d-z ,point)))
,@body))
|
(define (make-point3d . args) (apply list->vector args)) |
(define (make-adder a) (lambda (x) (+ x a))) (define add-7 (make-adder 7)) (define add-8 (make-adder 8)) (add-7 4) (add-8 4) |
(define (make-point3d x y z) (lambda () ???) |
(define (make-point3d x y z) (lambda (code) (code x y z))) (define (point3d-x point) (point (lambda (x y z) x))) (define (point3d-y point) (point (lambda (x y z) y))) (define (point3d-z point) (point (lambda (x y z) z))) (define-macro (with-point3d point . body) `(,point (lambda (x y z) ,@body))) |
(define (s+ . symbols)
(string->symbol (apply string-append
(map symbol->string symbols))))
(define-macro (define-type name . fields)
`(begin
(define (,(s+ 'make- name) ,@fields)
(lambda (code) (code ,@fields)))
,@(map (lambda (f)
`(define (,(s+ name '- f) type)
(type (lambda (,@fields) ,f)))) fields)
,(apply define-with-macro name fields)))
(define (define-with-macro name . fields)
`(define-macro (,(s+ 'with- name) type . body)
(list type (append (list 'lambda '(,@fields)) body))))
|
Хозяйке на заметкуВ вышеприведенном коде имеет смысл обратить внимание на участок с with-: мы имеем макрос, который генерирует другой макрос, который генерирует код :) При желании, подобным образом можно добавить дополнительные инструменты, вроде with-modify-. |
(define-type point3d x y z) |
(define-type avl-tree root less? equ?) |
(define (make-empty-avl-tree less? equ?) (make-avl-tree #f less? equ?)) |
(define-type avl-node key value l-child r-child l-depth r-depth) |
(define (avl-tree-insert tree key value)
(with-avl-tree tree
(make-avl-tree
(avl-tree-insert-node root key value less?)
less?
equ?)))
|
(define (avl-tree-insert-node node ckey cvalue less?)
(if (not node)
(make-avl-node ckey cvalue #f #f 0 0)
(let ((args (list node ckey cvalue less?)))
(with-avl-node node
(if (less? ckey key)
(apply avl-subtree-insert-node
make-left l-child l-depth args)
(apply avl-subtree-insert-node
make-right r-child r-depth args))))))
(define (avl-subtree-insert-node make-proc child depth node . args)
(let ((new-child (apply avl-tree-insert-node child args)))
(with-avl-node new-child
(make-proc node new-child (calc-depth new-child)))))
|
(define (make-left node child depth)
(with-avl-node node
(make-avl-node key value child r-child depth r-depth)))
(define (make-right node child depth)
(with-avl-node node
(make-avl-node key value l-child child l-depth depth)))
|
(define (calc-depth node) (with-avl-node node (1+ (max l-depth r-depth)))) |
|
Рис. 1: добавление элемента |
Хозяйке на заметкуЕсли быть точным, то высота AVL-дерева ограничена сверху значением 1.44 * log2N. |
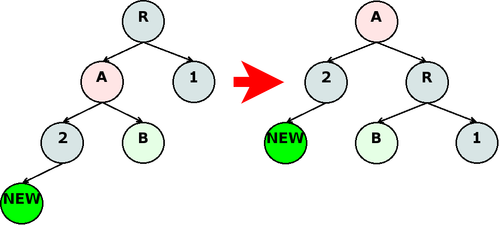 Рис. 2: правая ротация |
--- 1,11 ----
(define (avl-tree-insert-node node ckey cvalue less?)
(if (not node)
(make-avl-node ckey cvalue #f #f 0 0)
+ (avl-tree-check-rotate
(let ((args (list node ckey cvalue less?)))
(with-avl-node node
(if (less? ckey key)
(apply avl-subtree-insert-node
make-left l-child l-depth args)
(apply avl-subtree-insert-node
! make-right r-child r-depth args)))))))
|
(define (avl-tree-check-rotate node)
(with-avl-node node
(cond ((and (> l-depth r-depth)
(> (- l-depth r-depth) 1))
(apply avl-tree-rotate node rotate-right-set))
((and (> r-depth l-depth)
(> (- r-depth l-depth) 1))
(apply avl-tree-rotate node rotate-left-set))
(else node))))
(define rotate-right-set (list make-right
avl-node-l-child
make-left
avl-node-r-child
avl-node-r-depth))
(define rotate-left-set (list make-left
avl-node-r-child
make-right
avl-node-l-child
avl-node-l-depth))
(define (avl-tree-rotate node make-a get-child-a make-b get-child-b get-depth-b)
(let* ((child-a (get-child-a node))
(child-b (get-child-b child-a))
(depth-b (get-depth-b child-a)))
(let ((new-node (make-b node child-b depth-b)))
(make-a child-a new-node (calc-depth new-node)))))
|
(define (fill list)
(fold (lambda (k t) (avl-tree-insert t k #t))
(make-empty-avl-tree < =)
list))
|
(calc-depth (avl-tree-root (fill (unfold 0 (lambda (x) (>= x 1e6)) 1+)))) |
(define (avl-tree-lookup tree ckey)
(with-avl-tree tree
(let lookup ((node root))
(if (not node)
#f
(with-avl-node node
(cond ((equ? ckey key) value)
((less? ckey key) (lookup l-child))
(else (lookup r-child))))))))
|
Хозяйке на заметкуСтрого говоря, если вдаваться немного в подробности, в функциональном программировании есть интересный трюк, благодаря которому такой процесс протаскивания контенста можно автоматизировать и скрыть с глаз вообще, называется: "Монада". Но про монады я, пожалуй, расскажу в другой статье, а пока мы реализуем обход дерева в рамках fold. |
(define (avl-tree-fold tree proc acc)
(with-avl-tree tree
(let traverse ((node root) (c-acc acc))
(if (not node)
c-acc
(with-avl-node node
(let* ((l-val (traverse l-child c-acc))
(c-val (proc key value l-val))
(r-val (traverse r-child c-val)))
r-val))))))
|
(define (avl-tree-max-value tree) (avl-tree-fold tree (lambda (k v a) (max v a)) 0)) |
(define (avl-tree-double-copy tree)
(avl-tree-fold tree
(lambda (k v t) (avl-tree-insert t (* k 2) v))
(make-empty-avl-tree (avl-tree-less? tree)
(avl-tree-equ? tree))))
|
(define (avl-tree-insert tree key value)
(avl-tree-replace tree key (lambda (x) value)))
(define (avl-tree-replace tree key value-proc)
(with-avl-tree tree
(make-avl-tree
(avl-tree-insert-node root key value-proc less? equ?)
less?
equ?)))
|
--- 1,22 ----
! (define (avl-tree-insert-node node ckey value-proc less? equ?)
(if (not node)
! (make-avl-node ckey (value-proc #f) #f #f 0 0)
(avl-tree-check-rotate
! (let ((args (list node ckey value-proc less? equ?)))
(with-avl-node node
! (cond ((equ? ckey key)
! (make-avl-node key (value-proc value) l-child r-child l-depth r-depth))
! ((less? ckey key)
(apply avl-subtree-insert-node
make-left l-child l-depth args))
! (else
(apply avl-subtree-insert-node
make-right r-child r-depth args))))))))
|
(define-type queue left-list right-list length) (define (make-empty-queue) (make-queue '() '() 0)) |
(define (queue-empty? queue) (zero? (queue-length queue))) |
(define (queue-insert queue element)
(with-queue queue
(make-queue left-list
(cons element right-list)
(1+ length))))
|
(define-type remove-result
value
queue)
(define (queue-remove queue)
(with-queue queue
(cond ((zero? length) (make-remove-result #f queue))
((null? left-list)
(queue-remove (make-queue (reverse right-list)
'()
length)))
(else (make-remove-result (car left-list)
(make-queue (cdr left-list)
right-list
(1- length)))))))
|
(define (list->queue list)
(fold (lambda (e q) (queue-insert q e))
(make-empty-queue)
list))
(define (queue->list queue)
(let traverse ((queue queue) (list '()))
(if (queue-empty? queue)
(reverse list)
(with-remove-result (queue-remove queue)
(traverse queue (cons value list))))))
|
(define (queue-filter queue check?)
(let traverse ((queue queue) (result-queue (make-empty-queue)))
(if (queue-empty? queue)
result-queue
(with-remove-result (queue-remove queue)
(traverse queue
(if (check? value)
(queue-insert result-queue value)
result-queue))))))
|
(define-type hash-vector
vector
hash-proc
equ?)
(define (avl-tree->hash-vector tree table-size hash-proc)
(let ((vector (make-vector table-size '()))
(hash-proc (lambda (x) (modulo (hash-proc x) table-size))))
(avl-tree-fold tree
(lambda (k v a)
(let* ((index (hash-proc k))
(cell (cons k v))
(list (vector-ref vector index)))
(vector-set! vector index (cons cell list))))
(void))
(make-hash-vector vector hash-proc (avl-tree-equ? tree))))
|
(define (assoc-ex key list =)
(cond ((null? list) #f)
((= key (caar list)) (car list))
(else (assoc-ex key (cdr list) =))))
(define (hash-vector-lookup hash-vector key)
(with-hash-vector hash-vector
(let* ((index (hash-proc key))
(list (vector-ref vector index))
(value (assoc-ex key list equ?)))
(if value (cdr value) #f))))
|
(define-type hash-tree
tree
size
table-size
hash-proc
equ?
load-factor)
(define (make-empty-hash-tree table-size hash-proc equ? load-factor)
(make-hash-tree (let loop ((index 0)
(tree (make-empty-avl-tree < =)))
(if (>= index table-size)
tree
(loop (1+ index)
(avl-tree-insert tree index '()))))
0
table-size
hash-proc
equ?
load-factor))
(define (hash-tree-resize htree new-size)
(with-hash-tree htree
(avl-tree-fold (hash-tree-tree htree)
(lambda (index list tree)
(fold (lambda (v t)
(hash-tree-insert t (car v) (cdr v)))
tree
list))
(make-empty-hash-tree new-size
hash-proc
equ?
load-factor))))
(define (hash-tree-insert htree key value)
(with-hash-tree htree
(if (>= (/ size table-size) load-factor)
(let ((new-tree (hash-tree-resize htree
(* table-size 2))))
(hash-tree-insert new-tree key value))
(make-hash-tree
(let ((index (modulo (hash-proc key) table-size)))
(avl-tree-replace tree
index
(lambda (list)
(cons (cons key value) list))))
(1+ size) table-size hash-proc equ? load-factor))))
(define (hash-tree-lookup htree key)
(with-hash-tree htree
(let* ((index (modulo (hash-proc key) table-size))
(list (avl-tree-lookup tree index))
(value (assoc-ex key list equ?)))
(if value (cdr value) #f))))
|
swizard
swizard@beercan.ru
swizard