Common Lisp как мета-язык

Введение

Любой человек, имеющий представление о CL, прекрасно знает, что этот язык отлично подходит для создания DSL. К тому же, наверняка, многие слышали такую формулировку: "Common Lisp — это не язык программирования, это мета-язык, идеальное средство для создания своих языков". Тем не менее (насколько я могу судить по рунету) корректно раскрыть это понятие не может практически никто. Даже люди, непосредственно практикующие CL.

Обычно, когда речь заходит о широких возможностях по созданию DSL в лиспе, приводят в пример loop и format, предметно-ориентированные языки, для описания итеративных процессов и форматирования данных для отображения в поток (например, на экран). Разумеется, это корректные примеры, но в итоге создается ложное ощущение, что это максимум, на что способен CL.

В реальной жизни даже в коммон-лисповых проектах очень редко где можно посмотреть действительно хорошие примеры DSL. Одно из очень немногих таких мест — это компилятор SBCL (и, соответственно, CMUCL). Основная масса же штатных проектов минимально задействуют макросы, в основном, для RAII конструкций вида with-something ().


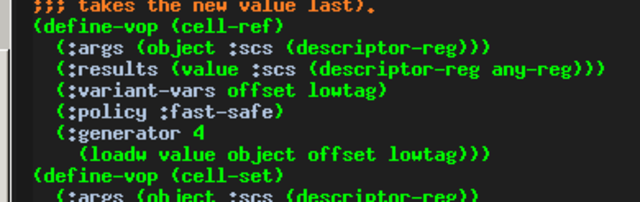
Компилятор SBCL активно использует DSL.

Большинство новых программистов, которые приходят к CL, вводятся в заблуждение относительной мультипарадигменностью языка. Часть их начинает экспериментировать с функциональным стилем, часть бросается писать биндинги к существующим библиотекам на других языках, часть начинает просто переписывать на CL какие-то традиционные проекты, активно пользуясь неродными для лиспа методиками и шаблонами проектирования. На таком мощном ЯП как лисп, все эти эксперименты имеют все шансы окончиться успешно, но в каждом конкретном случае новичок остается немного недоволен. Одним начинает не хватать обязательной типизации, другим нужен ленивый язык, третьих не устраивает малое количество уже написаных библиотек или расстраивает небольшой размер коммьюнити. В конце концов, очень многим просто не нравится синтаксис!

Я считаю, что освоение CL нужно начинать с того, в чем этот язык действительно силен: с проектирования собственных предметно-ориентированных языков. Цель данной статьи состоит в том, чтобы продемонстрировать, насколько это легко и приятно.

Постановка задачи

Самое сложное в процессе — это подобрать адекватную задачу. С одной стороны, она должна оказаться достаточно объемной и сложной, чтобы выгода от использования DSL стала очевидной каждому, с другой — достаточно простой, чтобы читателям не нужно было долго и муторно вникать в предметную область, с третьей — достаточно компактной, чтобы бы вышел вменяемым размер статьи. Мне это достаточно продолжительное время не удавалось, пока я не придумал, на мой взгляд, удачный вариант.

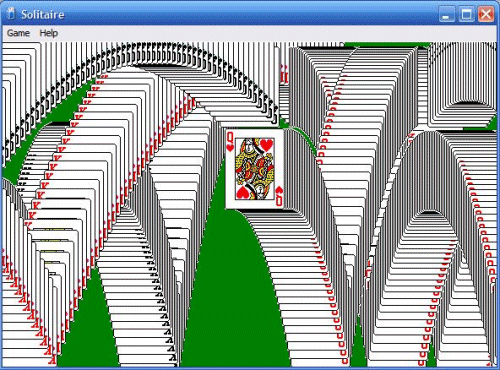
В рамках данного текста будет рассматриваться всем до боли известный проект: пасьянс "Косынка". Тот самый, на счету которого миллиарды часов жизни, украденных у офисного планктона.


Пасьянс "Косынка" во всей своей первобытной красе.

Мы реализуем нечто вроде "скрепки-помощника": программу, которая в трудную минуту может подсобить незадачливому клерку в игре, отобразив все возможные для данного расклада варианты ходов. Для упрощения реализации пусть приложение будет консольным, чтобы ворох кода, отвечающего за отрисовку GUI не погреб под собой собственно демонстрацию DSL. Например, готовая реализация для скриншота выше у меня выглядит как-то так: 

pile +STOCK0001+ with top card UNKNOWN
pile +WASTE0002+ with top card EMPTY
pile +FOUNDATION0003+ with top card EMPTY
pile +FOUNDATION0004+ with top card EMPTY
pile +FOUNDATION0005+ with top card EMPTY
pile +FOUNDATION0006+ with top card EMPTY
pile +TABLEAU0007+ with top card 2C
pile +TABLEAU0008+ with top card 3S
pile +TABLEAU0009+ with top card KS
pile +TABLEAU0010+ with top card 6S
pile +TABLEAU0011+ with top card TH
pile +TABLEAU0012+ with top card KH
pile +TABLEAU0013+ with top card QS
Choose an action: 
0 -- Quit
1 -- Reveal top on pile +STOCK0001+ with top card UNKNOWN; Move card from pile +STOCK0001+ with top card UNKNOWN to pile +WASTE0002+ with top card EMPTY
2 -- Move cards stack from pile +TABLEAU0013+ with top card QS at QS to pile +TABLEAU0012+ with top card KH

Можно особо в него не вчитываться -- не суть важно на что похож интерфейс.


Всегда можно расчитывать на помощь.

На всякий случай, более конкретно о пасьянсе, для которого мы пишем помощника:

Предметно-ориентированный язык

Подготовка

Как я и обещал, задача была подобрана таким образом, чтобы не пришлось писать длинное введение в предметную область, и можно было сразу перейти к делу. Вот этим мы сейчас и займемся, создав для оной предметной области специальный язык. Итак,

  1. % mkdir solitaire
  2. % touch solitaire/dsl.lisp
  3. % emacsclient -n solitaire/dsl.lisp
  4. Гордо печатаем в шапке (in-package :solitaire)
  5. В соседнем браузере открываем соответствующую статью для ориентира

Приготовления закончены, начинаем подло списывать с википедии с таким видом, как будто у нас уже есть необходимый нам DSL. Чтобы продемонстрировать, насколько близко к предметной области у нас получается результат, я буду сначала приводить код, а затем писать коментарии.

Игральные карты

;; Define cards
(slt/defcards (suites (S C H D))
              (ranks (A 2 3 4 5 6 7 8 9 T J Q K))
              (colors ((black (S C)) (red (H D)))))

Валет, дама, король, туз.

Как это ни удивительно, но пасьянс раскладывают игральными картами. Что мы вообще знаем об игральных картах? У игральной карты есть масть: пики, червы, ну и так далее. По-вражески названия будут звучать как "Spades" ♠, "Clubs" ♣, "Hearts" ♥ и "Diamonds" ♦, отсюда и соответствующие сокращения: S, C, H, D. Далее, у карты есть достоинство: двойка, десятка, валет, etc. В описании ranks перечислены как (A 2 3 4 5 6 7 8 9 T J Q K)). Здесь имеется в виду "Ace", 2, 3, 4, 5, 6, 7, 8, 9, "Ten", "Jack", "Queen", "King", достоинства, расположенные по старшинству. Ну и последнее, что нам важно знать о карте -- ее цвет. Традиционно пики ♠ и крести ♣ считаются "черными", а червы ♥ и бубны ♦ -- "красными":

(colors ((black (S C)) (red (H D)))))

На этом декларация slt/defcards считается закрытой.

Поле для пасьянса

;; Define card piles 
(slt/defpiles (stock (24))
              (waste (0))
              (foundation (0 0 0 0))
              (tableau (1 2 3 4 5 6 7)))

Игровое поле, как оно есть.

Продолжаем списывать факты из википедии практически 1:1. Поле игры в клондайке представляет собой тринадцать стопок, между которыми по определенным правилам перекладываются карты, из одной стопки в другую. В некоторых стопках какое-то количество карт лежит с начала игры, в некоторые нам нужно сложить карты для победы. Вот эти стопки:

Собственно, думать тут особо не над чем, берем и записываем как есть.

Правила игры

В предыдущих 7 (семи) строчках кода мы определили карты и игральное поле. Теперь надо задать правила, по которым эти карты можно перекладывать, и у нас выйдет уже полноценная программа, задающая логику предметной области.

Над способом задания правил игры мне пришлось чуток поразмышлять, и, в итоге, я остановился на декларативном варианте, реализующем классический pattern matching по игровым условиям на поле. Шаблон у меня выглядит следующим образом:

(defmacro slt/defrule ((&rest |игровые условия|) &body |предпринимаемые действия|)
  ...)

Соответственно, программа должна проанализировать все заданные нами правила и, при совпадении условия с игровой ситуацией, предпринять заданные действия. По-сути, алгоритм должен пройтись по всем правилам, примеряя каждое условие каждого правила на текущий расклад. Если в каком-то правиле выполнятся все условия, то пользователю будет разрешено выполнить указанные действия. По-моему, получилось достаточно близко к предметной области (формальные правила игры в klondike).

Открываем карту в Stock и кладем в Waste

;; Reveal stock -> waste
(slt/defrule ((pile s stock) (pile w waste) (top-card c (on s) unknown))
  (reveal-top s)
  (move-top s w))
Turning only one card to the waste at a time, but only passing through the deck once. © wikipedia

Грубо говоря, эта декларация должна оказаться "переводом" с вышеприведенного английского на наш DSL. На деле получилось несколько многословней: нам следует указать, что "turning card" должно происходить только в случае наличия этой самой перевернутой карты, а само действие состоит из "переворота" и "перемещения". Но, тем не менее, все равно очень близко к оригиналу.

В синтаксической конструкции правила можно заметить, что при срабатывании очередного этапа условия возможна подстановка результата в переменную. Например, в рассматриваемом правиле мы подставляем совпадение "стопка равна stock" (pile s stock) в переменную s, которую затем можем использовать в другом условии: (top-card c (on s) unknown), где уточняется, что верхняя карта должна быть на стопке s. В то же время, эта верхняя карта оказывается в переменной c. Захват переменных при сопоставлении с образцом — это достаточно распространенная практика, и мы ей с удовольствием воспользуемся, так как она нам упростит жизнь в будущем.

Открываем карту на Tableau

;; Reveal tableau
(slt/defrule ((pile tb tableau) (top-card c (on tb) unknown))
  (reveal-top tb))

Пожалуй, самое простое правило. При наличие закрытой карты на верхушке tableau, ее, безусловно, можно вскрыть. Единственное, на что здесь стоит обратить внимание: стопка типа "tableau" будет матчить не какую-то конкретную, а вообще все стопки данного типа (на поле их семь). Этакий Prolog-style.

На пустое Tableau можно положить короля из Waste

;; Move King from waste to empty tableau
(slt/defrule ((pile w waste) (pile tb tableau) (top-card cw (on w) K) (top-card ct (on tb) empty))
  (move-top w tb))

Выбрав все карты с tableau, на освободившееся место можно положить короля, на базе которого затем будет возможно построить пирамиду. В данном правиле оговаривается, что короля можно взять с макушки Waste.

На пустое Tableau можно положить короля из другого Tableau

;; Move King stack from one tableau to empty another
(slt/defrule ((pile t1 tableau) (pile t2 tableau) (card c1 (on t1) K) (top-card c2 (on t2) empty))
  (move-stack t1 c1 t2))

С другой стороны, короля для основания Tableau можно достать из другого Tableau. Причем необязательно с макушки, можно из любого места стопки, при этом переместив весь получившийся стек.


На пустое Tableau можно переместить сразу стек карт с королем в основании.

Соответственно, следует иметь в виду, что условная конструкция (pile t1 tableau) ... (card c1 (on t1) K) дословно означает: "Если в одной из стопок Tableau среди открытых карт находится Король". Поэтому в target-языке (common lisp) это должно скомпилироваться в двойной цикл перебора: стопок + карт на стопках.

На пустое Tableau можно вернуть короля из Foundation

;; Move King back from foundation to empty tableau
(slt/defrule ((pile f foundation) (pile tb tableau) (top-card cf (on f) K) (top-card ct (on tb) empty))
  (move-top f tb))

И, чтобы закончить тему с королем в основании Tableau, нужно не забыть, что этого короля туда разрешается положить с макушки Foundation, если он там вдруг есть. На этом с королями все, можно переходить к другим пирамидам: в Foundation'ах.

В основание Foundation можно заложить туза

;; Move Ace from waste to empty foundation
(slt/defrule ((pile w waste) (pile f foundation) (top-card cw (on w) A) (top-card cf (on f) empty))
  (move-top w f))

;; Move Ace from tableau to empty foundation
(slt/defrule ((pile tb tableau) (pile f foundation) (top-card ct (on tb) A) (top-card cf (on f) empty))
  (move-top tb f))

Пирамида на Foundation строится в обратном направлении: с туза до короля, следовательно, нужно указать, что в случае пустого Foundation можно заложить этого туза в качестве фундамента.

В этих двух правилах я перечислил, откуда этого туза разрешено взять: с макушки Waste или какого-нибудь Tableau. В принципе, правилами не запрещается переложить туза с одного Foundation на другой, но я решил это правило опустить, иначе наша скрепка-помощник будет бесконечно мотать туза между пустыми Foundation'ами. Смысла в этом никакого, но, тем не менее, если есть желание, можете добавить данное правило самостоятельно.

Построение пирамиды на Tableau

;; Move card from waste to tableau
(slt/defrule ((pile w waste)
              (pile tb tableau)
              (top-card cw (on w))
              (top-card ct (on tb) (and (greater ct cw) (opposite-color ct cw))))
  (move-top w tb))

;; Move stack from one tableau to another
(slt/defrule ((pile t1 tableau)
              (pile t2 tableau)
              (card c1 (on t1))
              (top-card c2 (on t2) (and (greater c2 c1) (opposite-color c2 c1))))
  (move-stack t1 c1 t2))

;; Move card from foundation to tableau
(slt/defrule ((pile f foundation)
              (pile tb tableau)
              (top-card cf (on f))
              (top-card ct (on tb) (and (greater ct cf) (opposite-color ct cf))))
  (move-top f tb))

Карточная пирамида.

Итак, основные правила для выстраивания пирамиды на Tableau:

Собственно, ровно это и отображают три правила из нашего DSL-я. Первое разрешает брать карты для пирамиды из Waste, второе -- из другого Tableau, а третье позволяет возвращать в пирамиду на Tableau карты из Foundation. При этом при взятии карты из Tableau, разрешено двигать весь стек, основанием которого оказалась двигаемая карта.

Построение пирамиды на Foundation

;; Move card from waste to foundation
(slt/defrule ((pile w waste)
              (pile f foundation)
              (top-card cw (on w))
              (top-card cf (on f) (and (lesser cf cw) (same-suite cf cw))))
  (move-top w f))

;; Move card from tableau to foundation
(slt/defrule ((pile tb tableau)
              (pile f foundation)
              (top-card ct (on tb))
              (top-card cf (on f) (and (lesser cf ct) (same-suite cf ct))))
  (move-top tb f))

Вообще, цель всего пасьянса -- это построить четыре полные пирамиды на всех четырех Foundation'ах, по одной на каждую масть. Соответственно, правила там следующие:

Вышеприведенный код задает два правила, разрешающие брать карты для такой пирамиды из Waste и какого-нибудь Tableau соответственно.

Финальное условие: победа

;; Win condition
(slt/defrule ((pile s stock)
              (pile w waste)
              (pile tb tableau)
              (top-card cs (on s) empty)
              (top-card cw (on w) empty)
              (top-card ct (on tb) empty))
  (win))

Вжжжик, вввжжжик, вжжжжик!

В принципе, это условие можно задать по-разному. Я выбрал проверку, что все стопки, кроме Foundation опустели: это означает, что все карты из колоды перекочевали на свои целевые места. Можно пойти другим путем: проверить, что все карты на макушках у Foundation'ов являются королями -- это будет еще короче, и тоже даст желаемый результат. Это неважно, главное, что у нас под конец сформировался достаточно мощный DSL, позволяющий в рамках нашей предметной области описывать практически любые возможные ситуации.

Это и была наша цель.

Итоги раздела

Итогом раздела оказался файл dsl.lisp, который содержит в себе код на только что "изобретенном" нами предметно-ориентированном языке. В принципе, это совершенно полноценный алгоритм, описывающий правила игры в "Косынку". И пусть нам его пока нельзя выполнить, так как у нас нет для нашего нового языка компилятора, но зато суммарный объем логики уместился всего в ~70 значащих строчек кода.

За счет чего получилась такая компактность? За счет выразительности языка в пределах своей предметной области. И пусть на этом языке у нас не выйдет написать какой-нибудь сервер или анализатор логов, но зато программировать на нем правила игры в Klondike одно удовольствие.

Разумеется, можно спроектировать еще более компактный DSL для нашей задачи. Но, как мне кажется, с увеличением компактности мы начнем проигрывать в читаемости кода. Я это не проверял, поэтому, возможно, я и ошибаюсь. Если есть желание, можете поэкспериментировать сами.

Компилятор DSL

Суть компиляции

Если при слове "компилятор" вы представляете себе какой-нибудь монструозный gcc или (упаси Господь) Visual Studio, то в нашем случае можно спокойно расслабиться. Наш исходный язык (DSL) представляет собой корректный лисп, и целевой язык тоже является корректным лиспом. По-сути, весь наш процесс сводится к несложному преобразованию одних SEXP в другие, которые уже, в свою очередь, будут интерпретироваться или компилироваться в байт- или машинный код.

Допустимо компилятор рассматривать как совершенно независимый подпроект в рамках основного проекта: программу, которая получает на вход одни лисповые списки, и выдает на выходе другие. В принципе, можно провести аналогию с сишным препроцессором cpp, представляющим собой вполне самостоятельную утилиту, трансформирующую сишный код перед собственно генерацией ассемблера. Точно так же, макросистема common lisp является механизмом для программирования этапов обработки исходника перед его финальной компиляцией.


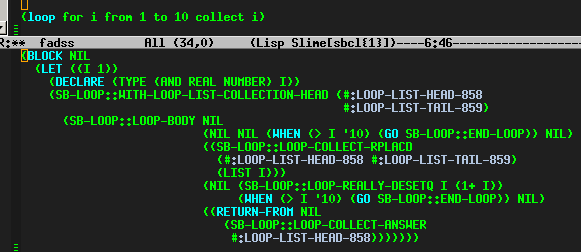
Результат MACROEXPAND простой конструкции LOOP.

Итак, главная цель нашего будущего компилятора: пребразовать DSL таким образом, чтобы результат оказался корректным кодом на коммон лиспе, который, к тому же, при выполнении делает то, что мы задумывали. И здесь имеет смысл отметить несколько основных моментов, за которые common lisp и заслужил себе славу мета-языка (или, языка-конструктора):

Конечно, это далеко не единственные бонусы, но без практических примеров это всего лишь расплывчатая теория. Поэтому перейдем к компилятору DSL "Косынка".

Подготовка

Компилятор будет обособлен в отдельном исходнике (в принципе, можно даже вынести его в самостоятельный пакет, но на такой мелкой задаче это необязательно).

  1. % touch solitaire/dsl-compiler.lisp
  2. % emacsclient -n solitaire/dsl-compiler.lisp
  3. Вписываем в шапку (in-package :solitaire)

На данном этапе подошло время для организационных работ для проекта. Причины две:

  1. Нужно четко указать компилятору порядок сборки проекта: dsl-compiler.lisp должен быть скомпилирован до dsl.lisp, иначе, безусловно, возникнут ошибки.
  2. Нам потребуется библиотека metatilities, чтобы не отвлекаться на самостоятельную имплементацию тривиальных функций вроде curry или compose.

Поэтому предлагаю добавить в проект файлы solitaire.asd и package.lisp, чтобы сразу получить рабочий asdf. Файл game.lisp будет рассмотрен в соответствующем разделе.

Можно переходить к компилятору.

slt/defcards

Напоминаю еще раз конструкцию:

;; Define cards
(slt/defcards (suites (S C H D))
              (ranks (A 2 3 4 5 6 7 8 9 T J Q K))
              (colors ((black (S C)) (red (H D)))))

Прежде чем писать трансформацию, следует прикинуть, чего мы вообще хотим реализовать, хотя бы самый минимум. Очевидно, что программа-помощник по раскладу пасьянса должна уметь:


Компилятор DSL просто трансформирует одни SEXP в другие.

Далее, следует определиться со вторым вопросом: каким образом карта будет представлен в реальной программе. Имеется в виду следующий момент: сравнивая масти двух карт, мы на деле сравниваем что? Значение полей двух структур? Строки? Числа? В принципе, не важно, как мы представляем себе карту, самое главное, чтобы мы придерживались выбранного соглашения везде в пределах компилятора конкретного DSL. На выбор:

Вариантов миллион, можно хоть CLOS object создать. Технически, может даже вообще не потребоваться никакого представления в целевом языке, если абстракция "схлопнется" на уровне раскрытия DSL. В этом (обращаю еще раз внимание) гибкость подхода с DSL: логические абстракции остаются в предметно-ориентированном языке, а вот конечный вид целевого языка можно выбирать, исходя из конкретных нужд и предпочтений.

В нашем случае я выбрал, может, и не самый удачный вариант в плане производительности результирующего кода, но, как мне кажется, самый выгодный в плане демонстрации возможностей DSL в лиспе. Карта у меня определяется соответствующим символом: '|7S| == 7♠.

Возникает закономерный вопрос: каким тогда образом мне понять, увидев на макушке стопки, допустим, 'KH, что это король? Что ж, если б я писал программу руками, я бы сделал это либо через хеш:

(eq (gethash card *suites*) 'K)

либо как-то так:

(char= (elt (symbol-name card) 0) #\K)

Но! Программу-то за меня пишет компьютер, а я ему всего лишь командую, как это делать. Поэтому правильный ответ будет звучать так:

(or (eq card 'KS) (eq card 'KC) (eq card 'KH) (eq card 'KD))

Неожиданный ход, не правда ли? Отдает индусятиной, но лишь для программистов, которые не практиковали раньше кодогенерацию. Проверка на масть будет содержать 13 условий под or. Проверка факта, что карту А можно положить на карту Б в пирамиде потребует соответствующей комбинации условий.


Кодогенерация и индусятина — это разные вещи.

В подобной кодогенерации нет ничего плохого, в большинстве случаев этот механизм заметно быстрее эквивалентного "ручного" кода. Разумеется, даже в этом случае следует быть внимательным, чтобы не напороться на комбинаторный взрыв. Например, чтобы с помощью кодогенерации условий обнаружить тот факт, что карта А той же масти, что и карта Б, придется сгенерировать ~680 проверок, что уже несколько напрягает, и желательно, все же, свернуть хотя бы часть до векторных сравнений, вроде #'subsetp:

SOLITAIRE> (let* ((suites '(S C H D))
                  (ranks '(A 2 3 4 5 6 7 8 9 T J Q K)))
             (gen-cards-check-suite (gen-cards ranks suites) 
                                    ranks))
(OR
 (SUBSETP (LIST CARD-A CARD-B)
          '(AS |2S| |3S| |4S| |5S| |6S| |7S| |8S| |9S| TS JS QS KS) :TEST #'EQ)
 (SUBSETP (LIST CARD-A CARD-B)
          '(AC |2C| |3C| |4C| |5C| |6C| |7C| |8C| |9C| TC JC QC KC) :TEST #'EQ)
 (SUBSETP (LIST CARD-A CARD-B)
          '(AH |2H| |3H| |4H| |5H| |6H| |7H| |8H| |9H| TH JH QH KH) :TEST #'EQ)
 (SUBSETP (LIST CARD-A CARD-B)
          '(AD |2D| |3D| |4D| |5D| |6D| |7D| |8D| |9D| TD JD QD KD) :TEST #'EQ))

Вернемся к синтаксису slt/defcards. Опираясь на данные, указанные нам пользователем (в смысле, нами же и указанными), следует сгенерировать соответствующие функции-хелперы для определения отношений двух карт: старше/младше, одинаковая ли масть/цвет и т.д. Вот как-то так (см. исходник):

(defmacro slt/defcards (&rest declarations)
  (destructuring-bind (ranks suites colors)
      (mapcar (curry #'assoc/error declarations) '(ranks suites colors))
    (let ((pairs (make-card-pairs suites ranks))
          (cards (gen-cards ranks suites)))
      (setf *ranks* ranks)
      (setf *cards* cards)
      `(progn
         (defun lesser (card-a card-b)
           ,(gen-cards-lesser pairs))
         (defun greater (card-b card-a)
           ,(gen-cards-lesser pairs))
         (defun opposite-color (card-a card-b)
           ,(gen-cards-opposite ranks colors))
         (defun same-color (card-a card-b)
           (not (opposite-color card-a card-b)))
         (defun same-suite (card-a card-b)
           ,(gen-cards-check-suite cards ranks))
         (defun check-card (card)
           ,(gen-cards-check cards))
         (defmacro check-rank (card-var rank)
           ,(gen-rank-check-macro ranks suites))))))
  1. assoc/error проверяет синтаксис на корректность.
  2. gen-cards склеивает собственно карточные символы из мастей и доcтоинств.
  3. make-card-pairs генерирует пары по старшинству достоинств.
  4. И, наконец, генерируются необходимые хелперы:
    • (lesser 7♠ 8♦) -> t. Это нам понадобится для составления пирамид на tableau.
    • (greater T♣ 9♥) -> t. Это нам понадобится для составления пирамид на foundation.
    • (same-color 7♠ A♣) -> t. Этот хелпер нам, на самом деле, ни за чем ни пригодится, я его случайно сгенерил.
    • (opposite-color 4♦ A♣) -> t. А это нам пригодится: для составления пирамид на tableau.
    • (same-suite 6♣ J♣) -> t. Соответственно, на foundation: в одну стопку складываются карты одинаковой масти.
    • (check-card 1♥) -> nil. Хелпер просто проверяет, существует ли такая карта: понадобится для проверки корректности ввода пользователя.
    • (check-rank card J) -> 
      (or (eq card 'JS) (eq card 'JC) (eq card 'JH) (eq card 'JD))
      Пригодится в DSL для проверки верхушек стопок: король ли там, или, может, туз.

Конкретная реализация предельно элементарна, и приводить прямо в статье ее смысла нет никакого. Можно взглянуть в исходник.

slt/defpiles

Напоминаю конструкцию:

;; Define card piles 
(slt/defpiles (stock (24))
              (waste (0))
              (foundation (0 0 0 0))
              (tableau (1 2 3 4 5 6 7)))

На самом деле, тут работы еще меньше. Для простоты стопки у нас будут лежать в plist в виде обычных списков. Карту рубашкой вверх мы обозначаем символом 'UNKNOWN, по мере переворачивания они будут заменяться стандартными символами соответствующих карт. Соответственно, нам понадобятся:

Собственно, все по компиляции поля для игры.


Вручную раскладывать заметно дольше.

slt/defrule

На всякий пожарный, еще раз конструкцию:

;; Reveal stock -> waste
(slt/defrule ((pile s stock) (pile w waste) (top-card c (on s) unknown))
  (reveal-top s)
  (move-top s w))

Что касается синтаксиса для объявления правил, то здесь образуется небольшая засада: в пределах DSL правила не сгруппированы, и мы свободно можем объявлять их в любом удобном месте. В связи с этим нам потребуется так называемая "двухпроходная" компиляция: на первой стадии мы собираем правила в кучу, а потом уже эту кучу превращаем в common lisp.

(defvar *rules* '())

(defun compile-conditions (action condition &rest conditions)
  (apply #'compile-condition action conditions condition))

(defmacro slt/defrule ((&rest conditions) &body body)
  (push (apply #'compile-conditions `(schedule-actions (list ,@body)) conditions) *rules*)
  'nil)

Здесь нет ничего сложного, но следует быть чуток повнимательней, так как нужно не запутаться в стадиях трансляции. Глобальная переменная *rules* заполняется на первой стадии компиляции slt/defrule (во время раскрытия макроса) — туда аккумулируются предварительно распарсеные и обработанные правила. Затем, на второй стадии, на основании данных в этой переменной генерируется функция run-rules, результат компиляции которой уже используется в основном игровом коде:

(defmacro slt/compile-rules ()
  `(defun run-rules () ,@*rules*))

Что должно представлять из себя оттранслированное правило? Логично предположить, что это должен быть код, который, при срабатывании указанных в правиле условий должен произвести указанные там же действия. И, если с действиями все понятно, то условия явно требуют от нас препроцессинга — они у нас заданы в стиле Prolog (условия сразу на множество). Например, такое правило не уточняет, какое именно tableau имеется в виду, поэтому оно обязано срабатывать на любом:

;; Reveal tableau
(slt/defrule ((pile tb tableau) (top-card c (on tb) unknown))
  (reveal-top tb))

В связи с этим в лиспе нам потребуется перебор указанных стопок, я его реализовал через mapc. Вот во что у меня транслируется подобное определение:

(MAPC
  (LAMBDA (TB)
    (MAPC
     (LAMBDA (C)
       (WHEN (EQ C 'UNKNOWN) (SCHEDULE-ACTIONS (LIST (REVEAL-TOP TB)))))
     (LIST (CAR (GETF *TABLE* TB)))))
  '(+TABLEAU0013+ +TABLEAU0012+ +TABLEAU0011+ +TABLEAU0010+ +TABLEAU0009+
    +TABLEAU0008+ +TABLEAU0007+))

Разумеется, выходит несколько неаккуратно, что я запускаю перебор даже для случаев, когда анализируется только один элемент в списке (в данном примере, верхушка стопки). И конечно же, перед написанием статьи я планировал это заоптимизировать (добавив третих проход, превращающий биндинг (mapc (lambda (var) ...) (list x)) в (let ((var x)) ...)), но к этому моменту я занимался уже какой-то другой занимательной задачкой, и мне стало тупо лень :) На деле же там нужно совсем мизер работы: заменить генерацию mapc на макрос, например, for-items, который определяется неким подобным образом:

(defmacro for-items ((bind &rest list) &body body)
  (if (> (length list) 1)
      `(mapc (lambda (,bind) ,@body) (list ,@list))
      `(let ((,bind ,(car list))) ,@body)))

Предлагаю читателям проделать это самостоятельно, тем более, что это совершенно волшебный пример того, как свободно на CL реализуются оптимизирующие компиляторы DSL.


"Premature optimization is the root of all evil", сказал он, но это явно не наш случай.

А пока моя реализация compile-condition выглядит так:

(defun compile-condition (action rest-conditions type bind &rest specs)
  (flet ((cond-continue () (apply #'compile-conditions action rest-conditions)))
    (ecase type
      (pile
       `(mapc (lambda (,bind) ,(if (null rest-conditions) 'nil (cond-continue)))
              '(,@(getf *piles* (car specs)))))
      ((or card top-card)
       (destructuring-bind ((on pile-bind) &rest card-conds)
           specs
         (ecase on
           (on `(mapc (lambda (,bind)
                        ,(append (apply #'compile-card-condition bind card-conds)
                                 (list (if (null rest-conditions) action (cond-continue)))))
                      ,(ecase type
                              (top-card `(list (car (getf *table* ,pile-bind))))
                              (card `(getf *table* ,pile-bind)))))))))))

(defun compile-card-condition (bind &optional card-cond)
  (if card-cond
      `(when ,(cond ((member card-cond '(empty unknown)) `(eq ,bind ',card-cond))
                    ((member card-cond *ranks*) `(check-rank ,bind ,card-cond))
                    (t card-cond)))
      `(progn)))

На этом по компилятору практически все. Оставшиеся хвосты рассмотрим в следующем разделе, который будет посвящен собственно реализации приложения.

Итоги раздела

Итогом раздела оказался файл dsl-compiler.lisp, который содержит в себе реализацию транслятора нашего DSL из предыдущего раздела в корректный Common Lisp код, способный выполнять полезную работу. По-сути, сгенерированный им код уже является (за вычетом интерактивной части) реализацией нашего приложения — скрепки-помощника для косынки.

И, несмотря на то, что полностью работающего кода у нас еще нет, уже можно делать некоторые весьма приятные выводы:

Далее, подобная развязка логики (DSL) и представления (compiler) дает нам широкие возможности по интеграции алгоритма в любый существующие проекты: достаточно лишь под каждый такой проект написать свой компилятор (или бэкенд к нему). В конце концов, можно даже оттранслировать в другой язык программирования.

Итак, нам осталось дописать только интерактивную часть, чтобы получить законченное приложение. Приступим.

Игровой код

Подготовка

Весь игровой код будет содержаться в исходнике game.lisp, поэтому давайте его организуем:

  1. % touch solitaire/game.lisp
  2. % emacsclient -n solitaire/game.lisp
  3. Вписываем в шапку (in-package :solitaire)

В asd-описании проекта отмечено, что этот файл следует компилировать последним. Причина понятна: к моменту, когда мы начинаем реализовать интерактивную часть (диалог с пользователем), у нас в зубах уже должно оказаться куча сгенерированного кода, который должен родиться из нашего DSL.

Что уже есть и что еще надо


Практически все готово.

Итак, что нам к настоящему моменту приготовил наш вежливый компилятор (dsl-compiler):

  1. Глобальную переменную *table*, в которой в виде plist'a организовано поле для игры
  2. Глобальную переменную *piles*, в которой перечислены сгенерированные символы, для обозначения стопок. Они служат, например, ключами в *table*.
  3. Функцию init-game, которая сбрасывает игровое поле
  4. Небольшой хвост от компилятора: глобальная переменная *rules* и макрос slt/compile-rules, который нам надо преобразовать в код.

Сразу, пока не забыли, займемся сразу последним пунктом:

;; Compile rules
(slt/compile-rules)

На этом компиляция правил завершена (мы получили функцию run-rules, и можно переходить к интерактивной части.

Игровой цикл

Он предельно прост и лаконичен.

(defun run-game ()
  (init-game)
  (let ((*force-win* nil))
    (declare (special *force-win*))
    (loop
       :do (let ((*moves* nil))
             (declare (special *moves*))
             (show-field)
             (run-rules)
             (if *force-win*
                 (format t "You win~%")
                 (if (null *moves*)
                     (progn (format t "You lost~%") (setf *force-win* t))
                     (choose-perform-move *moves*))))
       :until *force-win*)))
  1. Рисуем текущую ситуацию на поле.
  2. Запускаем run-rules, которая ситуацию анализирует и прикидывает, какие ходы можно совершить. Результат должен накопиться в специальной переменной *moves*.
  3. Проверяются условия выхода из игрового цикла: победа, в случае, если специальная переменная *force-win* обрела истину, и поражение, в случае, если run-rules не смогла придумать ни одного полезного хода.
  4. Производится интерактивная часть: диалог с пользователем и обработка его ответа.

Что касается отрисовки поля и интерактивной части, там нет ничего интересного (все детали можно найти в исходнике). Поэтому перейдем сразу к более любопытной части: что представляют собой данные в *moves*.

Игровой ход

Как мы помним, нам от пары dsl+компилятор досталась функция run-rules. Она анализирует текущую ситуацию на игровом поле, и прикидывает, какие условия, заданные нами в DSL, выполняются. Каждый такой случай при помощи schedule-actions записывается в *moves*.


Игровой ход.

Что представляет собой игровой ход, например, в этом правиле?

;; Reveal stock -> waste
(slt/defrule ((pile s stock) (pile w waste) (top-card c (on s) unknown))
  (reveal-top s)
  (move-top s w))

Здесь два действия: открыть верхушку стопки s и переместить ее на стопку w. Что здесь есть запись вида (reveal-top s)? Я решил особо не мудрствовать, и сделал этот синтаксис обычным вызовом функции, который возвращает список из двух элементов:

  1. Строка представляющая собой вменяемый текст, который описывающет, что должно произойти. Например, для (reveal '+stock001+) дескрипшн будет иметь примерный вид: 
    "Reveal top on pile +STOCK0001+ with top card UNKNOWN"
  2. Thunk, который, будучи вызванным, выполнит то действие, которое было описано в первом пункте.

Благодаря данному соглашению, интерактивная часть реализуется элементарно: отображаем пользователю дескрипшн в качестве пункта меню, и, если тот этот пункт выберет, зовем thunk.

Для упрощения реализации ходов, я ввел очередной DSL: defaction/piles и defaction/piles+card:

(defmacro defaction/piles (name (desc-fmt &rest piles) &body body)
  (gen-action name piles desc-fmt (mapcar (compose (curry #'cons 'describe-pile) #'list) piles) body))

(defmacro defaction/piles+card (name (desc-fmt pile-src base-card pile-dst) &body body)
  (gen-action name (list pile-src base-card pile-dst) desc-fmt
              `((describe-pile ,pile-src) base-card (describe-pile ,pile-dst)) body))

(defun gen-action (name args describe-fmt describe-args body)
  `(defun ,name ,args
     (list (format nil ,describe-fmt ,@describe-args)
           (lambda () ,@body))))

Теперь ходы можно, не напрягаясь, описывать в таком стиле:

(defaction/piles move-top ("Move card from ~a to ~a" pile-src pile-dst)
  (let ((card (pop (getf *table* pile-src))))
    (push card (getf *table* pile-dst))))

В принципе, для этой конкретной задачи DSL может показаться оверкиллом, но почему бы не спрограммировать красиво сразу, если в CL это практически не требует усилий? :)

На этом, пожалуй, все о реализации игрового процесса. Если остались какие-нибудь мелкие вопросы по коду, можно глянуть в исходник.

Итоги раздела

Итогом раздела оказался файл game.lisp, реализующий недостающий нам до полноценного приложения код. Даже в таком его небольшом объеме (~70 строк) мы ухитрились изобрести еще один DSL, для описания разрешенных в пасьянсе ходов.

Основной вывод здесь, наверное, следующий: если немного попрактиковаться в предлагаемом в этой статье подходу к программированию, через некоторое время глаз автоматически станет замечать обособленные области, для которых легко ввести предметно-ориентированный язык. Причем, сколь бы малыми они не были, это не важно — процесс построения DSL в Common Lisp настолько прост, что практически всегда это стоит того.

Заключение

Настало время проверить, что у нас вышло, и подвести итоги. Итак:

  1. Собираем проект: (asdf:oos 'asdf:load-op :solitaire)
  2. Запускаем игру: (solitaire:run-game)
  3. Открываем в соседнем окне klondike
  4. Следуем указаниям нашей скрепки-помощника и дублируем ее советы в реальной игре.

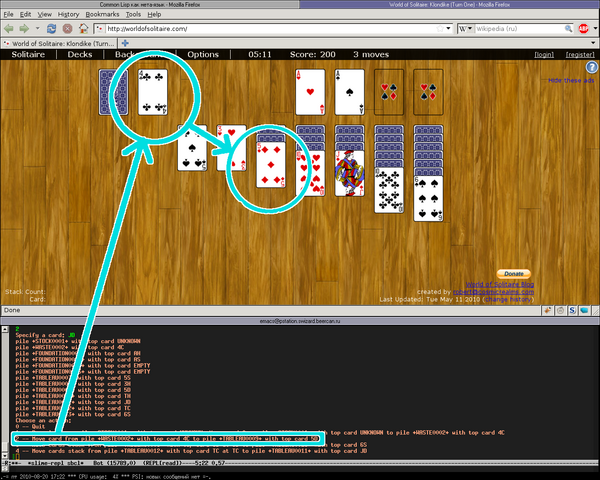
Помощник в действии (кликните для увеличения)

Надеюсь, в этой статье мне удалось продемонстрировать одну из сильнейших сторон CL: предметно-ориентированное программирование. Разумеется, подобный подход можно с успехом применять и в других языках: например, в Haskell можно реализовывать DSL, опираясь на его систему типов, а в Ruby — на мощные возможности ООП. Однако, нигде, кроме лиспа вы не получите столько легкости и свободы в этом благородном деле, здесь настолько благодатная почва, что предметно-ориентированные языки пишутся интуитивно :)

Если у вас есть какие-то комментарии или соображения по данной статье, я буду рад, если вы оставите их здесь.

© swizard

LiveJournal swizard

Jabber swizard@beercan.ru

Last.fm swizard